Escreva No Caderno Um Exemplo De FunçãO QuadráTica

Escreva No Caderno Um Exemplo De Função Quadrática: prepare-se para mergulhar no mundo das funções quadráticas, uma ferramenta poderosa para modelar o mundo ao nosso redor. Imagine um projétil sendo lançado no ar, a trajetória de um avião ou até mesmo a forma de um arco-íris.

Todas essas situações podem ser descritas por funções quadráticas, que, além de belas, são extremamente úteis.

Neste guia, vamos explorar o conceito de funções quadráticas, suas características e aplicações. Começaremos definindo o que são funções quadráticas e como identificá-las. Depois, vamos aprender a construir seus gráficos, analisando o vértice, a concavidade e as raízes.

Por fim, veremos exemplos práticos de como as funções quadráticas são usadas em diversas áreas do conhecimento, desde a física até a economia.

Introdução à Função Quadrática

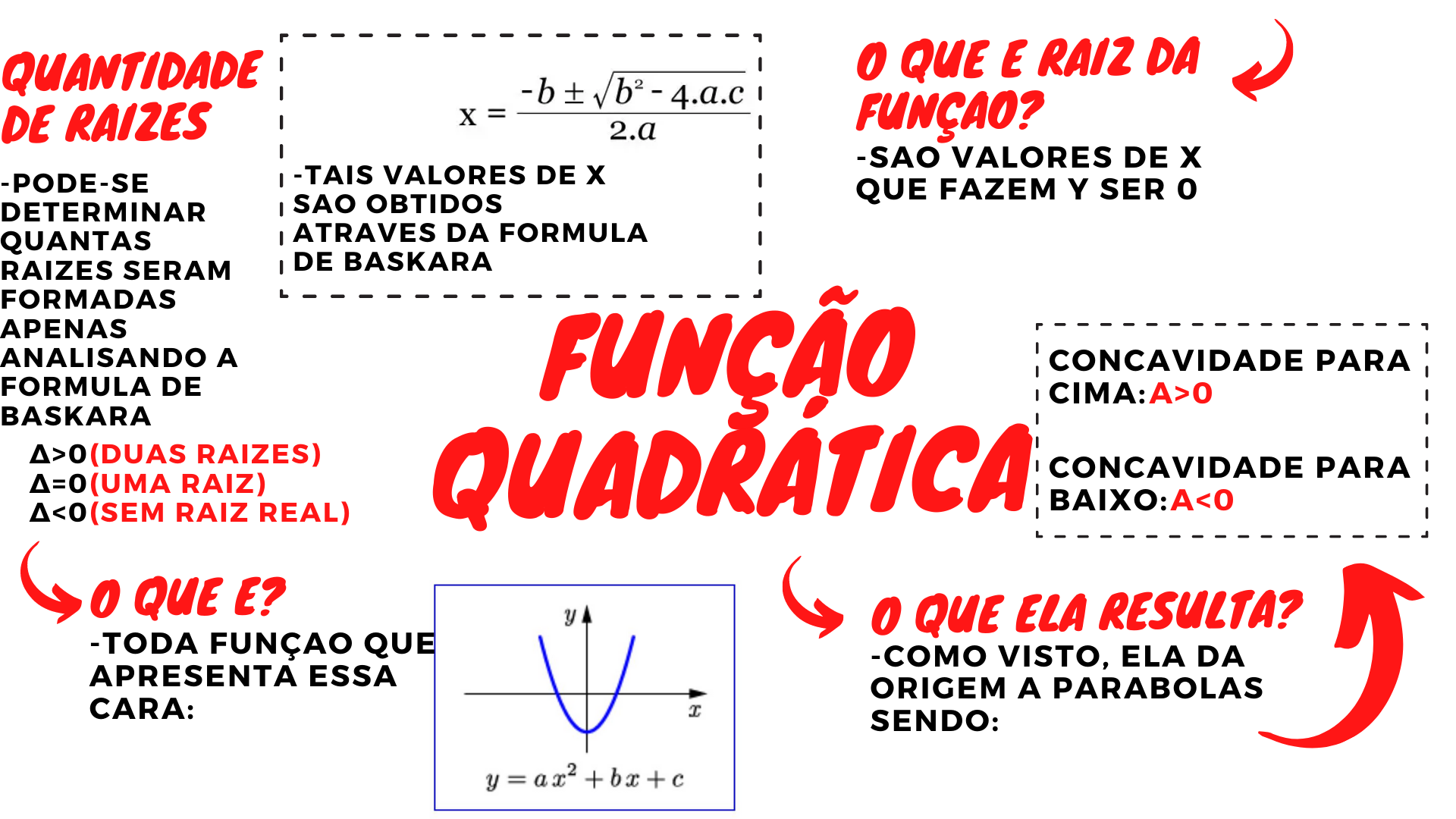
A função quadrática é um tipo de função matemática que descreve uma relação entre uma variável independente e uma variável dependente, onde a variável independente é elevada ao quadrado. É uma ferramenta fundamental em diversos campos, como física, economia e matemática, e seu estudo nos permite modelar e analisar fenômenos que seguem padrões parabólicos.

Forma Geral da Função Quadrática

A forma geral da função quadrática é dada pela expressão:

f(x) = ax² + bx + c

Onde:

• a, b e c são constantes reais, com a ≠ 0.
• x é a variável independente.
• f(x) é a variável dependente.

O coeficiente ‘a’ determina a concavidade da parábola, o coeficiente ‘b’ influencia a posição do vértice e o coeficiente ‘c’ representa o ponto de intersecção da parábola com o eixo y.

Características da Função Quadrática

As funções quadráticas possuem características únicas que as distinguem de outras funções matemáticas:

Gráfico da Função Quadrática

O gráfico de uma função quadrática é uma parábola, que pode ser aberta para cima ou para baixo, dependendo do sinal do coeficiente ‘a’.

Se ‘a’ > 0, a parábola é aberta para cima.

– Se ‘a’ < 0, a parábola é aberta para baixo.

Vértice da Parábola

O vértice da parábola é o ponto de mínimo ou máximo da função quadrática. Suas coordenadas são dadas por:

V = (-b/2a, f(-b/2a))

Concavidade da Parábola

A concavidade da parábola indica a direção em que a parábola se abre. A concavidade é determinada pelo sinal do coeficiente ‘a’:

Se ‘a’ > 0, a parábola é côncava para cima.

– Se ‘a’ < 0, a parábola é côncava para baixo.

Raízes da Função Quadrática

As raízes da função quadrática são os valores de x para os quais f(x) = Ou seja, são os pontos em que a parábola intersecta o eixo x. As raízes podem ser encontradas usando a fórmula quadrática:

x = (-b ± √(b²

4ac)) / 2a

Exemplos de Função Quadrática em Diferentes Contextos

As funções quadráticas são amplamente utilizadas em diversos campos, como:

Física

Lançamento de Projéteis

A trajetória de um objeto lançado no ar pode ser modelada por uma função quadrática. A altura do objeto em relação ao tempo é descrita por uma parábola.

Movimento Uniformemente Variado

A relação entre a velocidade de um objeto e o tempo, em um movimento uniformemente variado, pode ser representada por uma função quadrática.

Economia

Cálculo de Lucro

As funções quadráticas podem ser utilizadas para determinar o lucro máximo de uma empresa, em função da quantidade de produtos vendidos.

Modelagem de Demanda

A relação entre a demanda por um produto e seu preço pode ser modelada por uma função quadrática.

Matemática

Geometria Analítica

As funções quadráticas são usadas para descrever curvas e figuras geométricas, como parábolas e elipses.

Cálculo Diferencial e Integral

As funções quadráticas são ferramentas importantes no cálculo diferencial e integral, sendo utilizadas para calcular derivadas, integrais e áreas.

Representação Gráfica da Função Quadrática

A representação gráfica de uma função quadrática é um elemento fundamental para compreender seu comportamento e características. O gráfico de uma função quadrática é sempre uma parábola, uma curva simétrica com um ponto de mínimo ou máximo chamado vértice.

Construindo o Gráfico

Para construir o gráfico de uma função quadrática, podemos seguir os seguintes passos:

1. Encontrar o vértice

O vértice é o ponto de mínimo ou máximo da parábola. Para encontrá-lo, podemos usar a fórmula:

Vértice = (-b/2a, f(-b/2a))

Onde a, b e c são os coeficientes da função quadrática na forma f(x) = ax² + bx + c.

2. Encontrar as raízes

As raízes são os pontos onde a parábola intersecta o eixo x. Para encontrá-las, podemos usar a fórmula quadrática:

x = (-b ± √(b²

4ac)) / 2a

Se o discriminante (b²4ac) for positivo, a função terá duas raízes reais. Se o discriminante for zero, a função terá uma raiz real (uma raiz dupla). Se o discriminante for negativo, a função não terá raízes reais.

3. Encontrar o ponto de intersecção com o eixo y

O ponto de intersecção com o eixo y é o ponto onde a parábola intersecta o eixo y. Para encontrá-lo, podemos simplesmente substituir x = 0 na equação da função.

4. Plotar os pontos

Depois de encontrar o vértice, as raízes e o ponto de intersecção com o eixo y, podemos plotar esses pontos em um plano cartesiano e traçar a parábola que passa por esses pontos.

Métodos para Encontrar o Vértice, as Raízes e os Pontos de Intersecção, Escreva No Caderno Um Exemplo De Função Quadrática

Existem diferentes métodos para encontrar o vértice, as raízes e os pontos de intersecção de uma função quadrática. Além das fórmulas mencionadas acima, podemos usar:* Completando o quadrado:Essa técnica permite reescrever a equação da função quadrática na forma f(x) = a(xh)² + k, onde (h, k) representa o vértice.

Fatoração

Se a equação da função quadrática puder ser fatorada, podemos encontrar as raízes diretamente.

Gráfico

Podemos usar um gráfico para visualizar a parábola e encontrar o vértice, as raízes e os pontos de intersecção.

Comparando Gráficos de Diferentes Funções Quadráticas

A forma do gráfico de uma função quadrática depende dos coeficientes da equação. * Coeficiente a:O coeficiente a determina a abertura da parábola. Se a > 0, a parábola se abre para cima, e se a < 0, a parábola se abre para baixo. Quanto maior o valor absoluto de a, mais estreita a parábola. - Coeficiente b:O coeficiente b determina a posição horizontal do vértice.

Se b > 0, o vértice se move para a esquerda, e se b < 0, o vértice se move para a direita. - Coeficiente c:O coeficiente c determina a posição vertical do vértice. Se c > 0, o vértice se move para cima, e se c < 0, o vértice se move para baixo. Variando os coeficientes da equação, podemos obter diferentes formas de parábolas. Por exemplo, as funções f(x) = x² e f(x) = -x² têm a mesma forma, mas se abrem em direções opostas. A função f(x) = 2x² é mais estreita do que f(x) = x², e a função f(x) = x² + 1 está deslocada uma unidade para cima em relação a f(x) = x².

Aplicações da Função Quadrática: Escreva No Caderno Um Exemplo De Função Quadrática

A função quadrática, além de ser um conceito matemático importante, possui diversas aplicações práticas em diferentes áreas do conhecimento.

Ela pode ser utilizada para modelar fenômenos físicos, resolver problemas de otimização e até mesmo para entender o comportamento de sistemas complexos.

Aplicações em Fenômenos Físicos

A função quadrática é frequentemente utilizada para modelar o movimento de projéteis, como uma bola lançada ao ar. A trajetória de um projétil é descrita por uma parábola, que pode ser representada por uma função quadrática.

A equação que descreve o movimento de um projétil é dada por:y =

• (g/2)
• x² + v0
• x + y0

Onde:y é a altura do projétil em relação ao solox é a distância horizontal percorrida pelo projétilg é a aceleração da gravidadev0 é a velocidade inicial do projétily0 é a altura inicial do projétil

Outro exemplo de aplicação da função quadrática em física é o estudo de ondas. A forma de uma onda sonora, por exemplo, pode ser representada por uma função quadrática.

Aplicações em Otimização

A função quadrática também é utilizada para resolver problemas de otimização, como encontrar o ponto máximo ou mínimo de uma função.

Por exemplo, imagine uma empresa que deseja maximizar o lucro da venda de um produto. O lucro pode ser modelado por uma função quadrática, onde a variável independente é a quantidade de produtos vendidos. O ponto máximo da função quadrática representará a quantidade de produtos que deve ser vendida para maximizar o lucro.

Em outras áreas, como engenharia e economia, a função quadrática é utilizada para modelar e otimizar diversos processos.

Exercícios Práticos

Agora que você já aprendeu sobre a função quadrática, vamos colocar em prática o que aprendemos com alguns exercícios! Aqui, você vai aprender a determinar a equação, vértice, raízes e concavidade de uma função quadrática, além de ver como ela pode ser aplicada na resolução de problemas do dia a dia.

Exemplo de Função Quadrática

Vamos criar um exemplo de função quadrática e determinar suas características:

f(x) = 2x²

4x + 1

* Equação:A equação da função já está apresentada acima.

Vértice

Para encontrar o vértice, podemos usar a fórmula:

x_v =

b / 2a

y_v = f(x_v)

Onde

• a* e
• b* são os coeficientes da função quadrática. Neste caso,
• a* = 2 e
• b* =
• Substituindo na fórmula, temos:

x_v =

• (-4) / (2
• 2) = 1

y_v = f(1) = 2(1)²

• 4(1) + 1 =
• 1

Portanto, o vértice da função é (1,1).

• Raízes

  As raízes da função quadrática são os valores de

• x* que fazem
• f(x)* =
• Para encontrá-las, podemos usar a fórmula de Bhaskara:

x = (-b ± √(b²

4ac)) / 2a

Onde

• a*,
• b* e
• c* são os coeficientes da função quadrática. Neste caso,
• a* = 2,
• b* =
• 4 e
• c* =
• Substituindo na fórmula, temos:

x = (4 ± √((-4)²

• 4
• 2
• 1)) / (2
• 2)

x = (4 ± √8) / 4

x = (4 ± 2√2) / 4

x = 1 ± √2 / 2

Portanto, as raízes da função são:

x₁ = 1 + √2 / 2

x₂ = 1

√2 / 2

* Concavidade:A concavidade da função é determinada pelo sinal do coeficiente

• a*. Se
• a* > 0, a parábola é côncava para cima. Se

-a* < 0, a parábola é côncava para baixo. Neste caso, -a* = 2, portanto a parábola é côncava para cima.

Problema Prático

Imagine que você está jogando uma bola para cima. A altura da bola em relação ao solo, em função do tempo, pode ser representada por uma função quadrática. Vamos supor que a função que descreve a altura da bola seja:

h(t) =

5t² + 20t + 1

Onde

• h(t)* representa a altura da bola em metros e
• t* representa o tempo em segundos.

Utilizando essa função, podemos determinar:* A altura máxima atingida pela bola:O ponto máximo da parábola representa a altura máxima da bola. Para encontrá-lo, precisamos determinar o vértice da função. Usando a fórmula do vértice:

t_v =

• b / 2a =
• 20 / (2
• 5) = 2

h(t_v) = h(2) =

5(2)² + 20(2) + 1 = 21

Portanto, a altura máxima atingida pela bola é de 21 metros.

O tempo que a bola leva para atingir o solo

A bola atinge o solo quando

• h(t)* =
• Para encontrar o tempo, precisamos resolver a equação:

5t² + 20t + 1 = 0

Usando a fórmula de Bhaskara, encontramos as raízes da equação:

t = (-20 ± √(20²

• 4
• 5
• 1)) / (2
• 5)

t = (-20 ± √420) /

10

t = (-20 ± 2√105) /

10

t = 2 ± √105 / 5

Como o tempo não pode ser negativo, a solução válida é:

t = 2 + √105 / 5 ≈ 4.05 segundos

Portanto, a bola leva aproximadamente 4.05 segundos para atingir o solo.

Após explorarmos o mundo das funções quadráticas, você estará pronto para resolver problemas do mundo real e modelar fenômenos com mais precisão. Entender a função quadrática é como ter uma nova lente para olhar o mundo, descobrindo padrões e relações que antes passavam despercebidos.

Então, pegue seu caderno, sua caneta e embarque nesta aventura matemática!