Exemplo De Equação Do 1 Grau Para Representar No Gráfico é um conceito fundamental na matemática, que permite visualizar e analisar relações lineares entre variáveis. Através da representação gráfica, podemos obter insights sobre a inclinação, intersecção com os eixos e comportamento da equação, tornando-a uma ferramenta poderosa para a resolução de problemas em diversas áreas do conhecimento.
Equações do 1º grau são expressões matemáticas que envolvem uma variável elevada à primeira potência. Sua forma geral é representada por y = mx + b, onde m é o coeficiente angular, b é o coeficiente linear, x é a variável independente e y é a variável dependente.
A representação gráfica de uma equação do 1º grau resulta em uma linha reta no plano cartesiano, permitindo a visualização da relação entre as variáveis e a identificação de suas propriedades.
Introdução
Uma equação do 1º grau é uma expressão matemática que representa uma relação linear entre duas variáveis. Essas equações são essenciais para a compreensão de diversos conceitos matemáticos e possuem aplicações práticas em áreas como física, economia e engenharia. A representação gráfica de uma equação do 1º grau é uma ferramenta poderosa que permite visualizar a relação entre as variáveis e obter insights sobre o comportamento da equação.
Conceito de Equação do 1º Grau
Uma equação do 1º grau é uma equação que pode ser escrita na forma geral ax + b = 0, onde a e b são constantes e x é a variável. A característica principal de uma equação do 1º grau é que a variável x aparece apenas com expoente 1.
Essa equação representa uma reta no plano cartesiano.
Importância da Representação Gráfica
A representação gráfica de uma equação do 1º grau permite visualizar a relação entre as variáveis x e y de forma clara e intuitiva. Através do gráfico, podemos identificar facilmente o coeficiente angular e o coeficiente linear da equação, além de observar o comportamento da reta e sua intersecção com os eixos coordenados.
Definição de Equação do 1º Grau
Uma equação do 1º grau é uma equação que pode ser escrita na forma geral ax + b = 0, onde:
- a é o coeficiente angular, que determina a inclinação da reta;
- b é o coeficiente linear, que determina o ponto de intersecção da reta com o eixo y;
- x é a variável independente;
- y é a variável dependente.
Exemplos de Equações do 1º Grau: Exemplo De Equação Do 1 Grau Para Representar No Gráfico
Exemplo 1: Equação Simples
Considere a equação 2x + 4 = 0. Para resolver essa equação, precisamos isolar a variável x:
- Subtraia 4 de ambos os lados da equação: 2x + 4
- 4 = 0
- 4;
- Simplifique a equação: 2x =
4;
- Divida ambos os lados da equação por 2: 2x/2 =
4/2;
- Simplifique a equação: x =
2.
Portanto, a solução da equação 2x + 4 = 0 é x = -2.
Exemplo 2: Equação Mais Complexa
Considere a equação 3x- 5 = 7x + 1 . Para resolver essa equação, precisamos isolar a variável x:
- Subtraia 7x de ambos os lados da equação: 3x
- 5
- 7x = 7x + 1
- 7x;
- Simplifique a equação:
- 4x
- 5 = 1;
- Adicione 5 a ambos os lados da equação:
- 4x
- 5 + 5 = 1 + 5;
- Simplifique a equação:
4x = 6;
- Divida ambos os lados da equação por
-4
4x/-4 = 6/-4;
- Simplifique a equação: x =
1.5.
Portanto, a solução da equação 3x – 5 = 7x + 1 é x = -1.5.
Representação Gráfica de Equações do 1º Grau
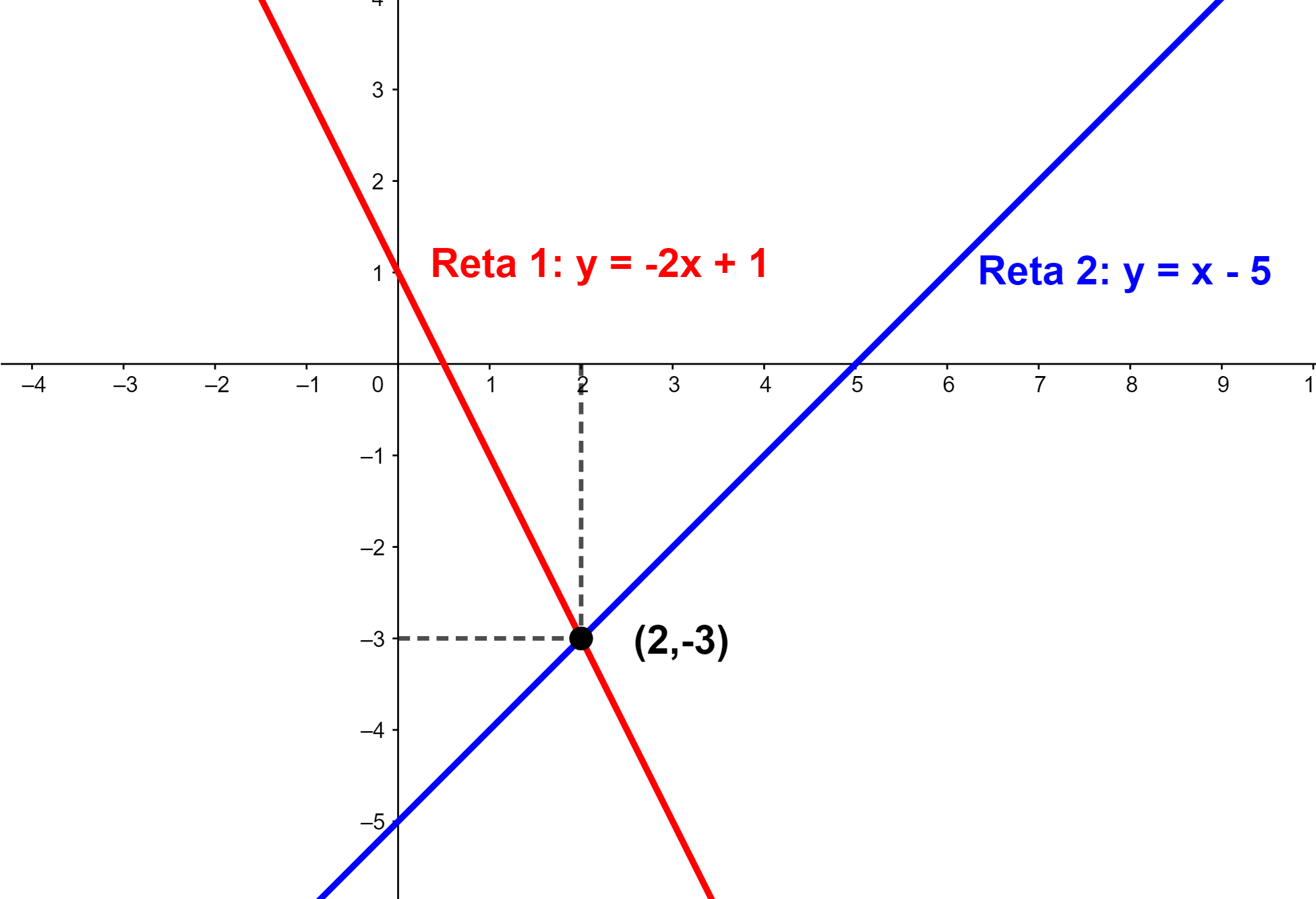
Método de Representação Gráfica
Para representar graficamente uma equação do 1º grau, precisamos encontrar dois pontos que satisfaçam a equação. Esses pontos serão plotados no plano cartesiano, e a reta que passa por esses pontos representará a equação.
Passos para Construir um Gráfico
Os passos para construir um gráfico de uma equação do 1º grau são:
- Escolher dois valores para x;
- Substituir esses valores na equação para encontrar os valores correspondentes de y;
- Criar uma tabela com as colunas x, y e (x, y);
- Plotar os pontos (x, y) no plano cartesiano;
- Traçar uma reta que passa por esses pontos.
Exemplo Passo a Passo
Considere a equação y = 2x + 1. Vamos construir o gráfico dessa equação:
- Escolhemos dois valores para x: x = 0 e x = 1;
- Substituímos esses valores na equação para encontrar os valores correspondentes de y:
- Para x = 0: y = 2(0) + 1 = 1;
- Para x = 1: y = 2(1) + 1 = 3;
- Criamos uma tabela com os valores de x, y e (x, y):
- Plotamos os pontos (0, 1) e (1, 3) no plano cartesiano;
- Traçamos uma reta que passa por esses pontos.
| x | y | (x, y) |
|---|---|---|
| 0 | 1 | (0, 1) |
| 1 | 3 | (1, 3) |
O gráfico resultante será uma reta com inclinação positiva, interceptando o eixo y no ponto (0, 1).
Análise da Representação Gráfica
Interpretação do Gráfico
A representação gráfica de uma equação do 1º grau fornece informações importantes sobre a equação. A inclinação da reta representa o coeficiente angular, que indica a taxa de variação de y em relação a x. O ponto de intersecção da reta com o eixo y representa o coeficiente linear, que indica o valor de y quando x é igual a zero.
Coeficiente Angular e Inclinação
O coeficiente angular da equação do 1º grau é representado pela letra a na forma geral ax + b = 0. Ele determina a inclinação da reta no gráfico. Um coeficiente angular positivo indica uma reta crescente, enquanto um coeficiente angular negativo indica uma reta decrescente.
Quanto maior o valor absoluto do coeficiente angular, maior a inclinação da reta.
Coeficiente Linear e Intersecção com o Eixo Y
O coeficiente linear da equação do 1º grau é representado pela letra b na forma geral ax + b = 0. Ele determina o ponto de intersecção da reta com o eixo y. O valor de b corresponde ao valor de y quando x é igual a zero.
Portanto, o ponto (0, b) é sempre um ponto que pertence à reta representada pela equação.
Aplicações de Equações do 1º Grau
Aplicações em Diferentes Áreas
As equações do 1º grau são amplamente utilizadas em diversas áreas do conhecimento, como:
- Matemática:Para resolver problemas de álgebra, geometria e cálculo;
- Física:Para modelar movimentos, calcular velocidades e analisar forças;
- Economia:Para analisar custos, receitas e lucros;
- Engenharia:Para projetar estruturas, calcular tensões e analisar sistemas.
Exemplos de Problemas Reais
Alguns exemplos de problemas reais que podem ser resolvidos com equações do 1º grau incluem:
- Calcular o preço final de um produto com desconto;
- Determinar a velocidade média de um veículo;
- Calcular o tempo necessário para percorrer uma distância específica;
- Analisar a relação entre o número de horas trabalhadas e o salário recebido.

