Regra de Três Simples: Como Fazer, Exemplos – Prepara Enem. A jornada para dominar a regra de três simples começa agora! Imagine-se desvendando os mistérios dos problemas matemáticos do ENEM com facilidade e confiança. Esta não é apenas uma fórmula; é a chave para abrir portas para o sucesso. Prepare-se para mergulhar em um universo de proporções, onde grandezas se relacionam e soluções surgem de forma elegante e intuitiva.
Vamos juntos desvendar os segredos dessa ferramenta poderosa e essencial para sua aprovação.
Neste guia completo, exploraremos os conceitos fundamentais da regra de três simples, diferenciando os tipos direto e inverso. Veremos como identificar a proporcionalidade em diferentes problemas, desde os mais básicos até aqueles que exigem um raciocínio mais aguçado. Através de exemplos práticos e questões do ENEM resolvidas passo a passo, você construirá uma base sólida e aprenderá a aplicar a regra de três simples em diversas situações cotidianas, da receita de bolo à economia de combustível.
Resolvendo Problemas com Regra de Três Simples no ENEM
A Regra de Três Simples, ferramenta aparentemente simples, se revela uma poderosa aliada na jornada rumo ao sucesso no ENEM. Dominá-la significa desvendar com elegância e eficiência uma gama considerável de questões, muitas vezes disfarçadas sob enunciados complexos. Prepare-se para transformar desafios em oportunidades de demonstração de conhecimento e raciocínio lógico.
Tipos de Problemas do ENEM que Utilizam Regra de Três Simples

No universo das provas do ENEM, a regra de três simples surge em diferentes contextos, vestindo-se com roupagens variadas para testar a sua capacidade de interpretação e aplicação. Encontrá-la-emos em problemas envolvendo proporcionalidade direta e inversa, em questões de escala, porcentagens, razões e taxas de variação, entre outros. A chave para o sucesso reside na habilidade de identificar a relação entre as grandezas apresentadas e estabelecer a proporção correta.
Exemplos de Questões do ENEM Resolvidas Passo a Passo
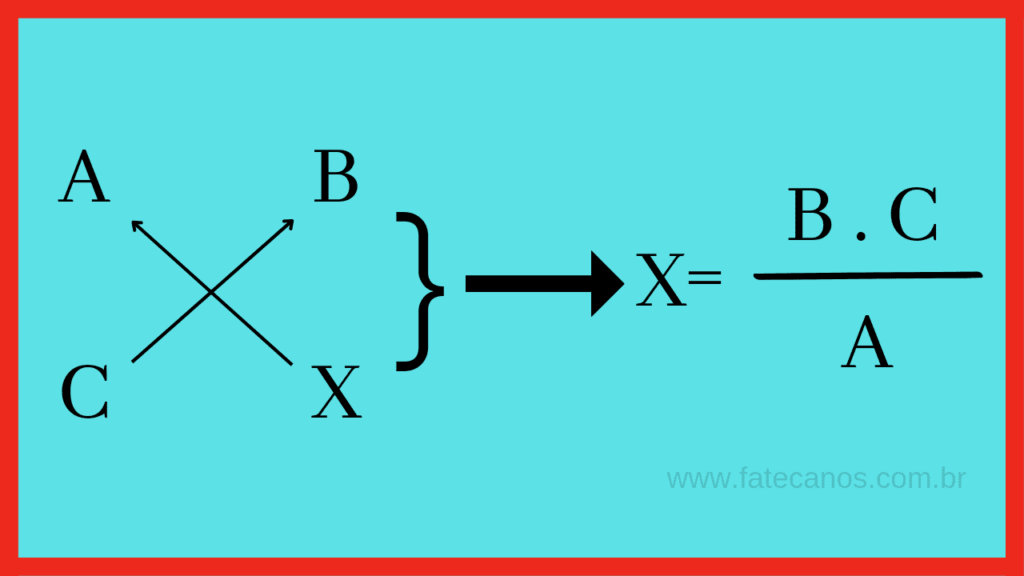
Vamos desvendar o mistério por trás de alguns exemplos concretos. Imagine uma questão sobre o consumo de combustível de um carro: “Um carro percorre 15 km com 1 litro de gasolina. Quantos litros serão necessários para percorrer 135 km?”. Aqui, temos uma relação de proporcionalidade direta: quanto maior a distância, maior o consumo de combustível. Podemos montar a regra de três:
- km —- 1 litro
- km —- x litros
Resolvendo: 15x = 135 => x = 9 litros. Simples, porém eficaz. Outro exemplo poderia envolver a diluição de uma solução: “Para preparar um determinado suco, utiliza-se 3 partes de água para 1 parte de concentrado. Se forem usados 120ml de concentrado, quantos ml de água serão necessários?”. Neste caso, a regra de três também se aplica diretamente:
- parte concentrado —- 3 partes água
- ml concentrado —- x ml água
Resolvendo: x = 360 ml de água.
Comparação entre Grandezas Diretamente e Inversamente Proporcionais
A distinção entre grandezas diretamente e inversamente proporcionais é crucial. Em grandezas diretamente proporcionais, o aumento de uma grandeza implica o aumento da outra na mesma proporção (e vice-versa). Já em grandezas inversamente proporcionais, o aumento de uma implica a diminuição da outra. Um exemplo clássico de grandeza inversamente proporcional é o tempo e a velocidade: quanto maior a velocidade, menor o tempo necessário para percorrer uma determinada distância.
Identificar corretamente esse tipo de relação é fundamental para a correta aplicação da regra de três.
Guia Passo a Passo para Resolver Problemas de Regra de Três Simples, Regra De Três Simples: Como Fazer, Exemplos – Prepara Enem

Para navegar com segurança pelo universo dos problemas de regra de três simples, siga estes passos:
1. Identifique as grandezas
Determine quais são as grandezas envolvidas no problema e suas unidades de medida.
2. Estabeleça a relação de proporcionalidade
Verifique se as grandezas são diretamente ou inversamente proporcionais.
3. Monte a regra de três
Organize as grandezas em forma de proporção, utilizando uma incógnita (x) para representar o valor desconhecido.
4. Resolva a equação
Multiplique os termos em cruz e isole a incógnita (x) para encontrar a solução.
5. Verifique a resposta
Analise se a resposta obtida faz sentido no contexto do problema.
Lembre-se: A prática leva à perfeição! Resolva diversos exercícios para consolidar seu aprendizado e aprimorar sua capacidade de identificar e resolver problemas de regra de três simples com maestria.
Aplicando a Regra de Três Simples em Situações Cotidianas: Regra De Três Simples: Como Fazer, Exemplos – Prepara Enem

A regra de três simples, ferramenta aparentemente simples da matemática, revela-se uma aliada poderosa em nosso cotidiano, facilitando decisões e cálculos em diversas situações. Sua aplicação prática transcende os muros da sala de aula, tornando-se um instrumento valioso para lidarmos com os desafios do dia a dia, desde o planejamento de uma receita até a economia de combustível em uma viagem.
Dominá-la significa ganhar agilidade e precisão em tarefas rotineiras, otimizando tempo e recursos.A regra de três simples nos permite estabelecer relações de proporcionalidade entre grandezas, encontrando valores desconhecidos a partir de informações conhecidas. Imagine-a como uma ponte que conecta o que sabemos com o que precisamos descobrir, guiando-nos com precisão e eficiência. Essa habilidade, aparentemente pequena, abre portas para uma compreensão mais profunda do mundo ao nosso redor, permitindo-nos tomar decisões mais informadas e estratégicas.
Exemplos de Aplicação em Situações Cotidianas
A regra de três simples surge em situações corriqueiras, muitas vezes sem que sequer percebamos. Vamos explorar alguns exemplos concretos para ilustrar sua utilidade prática. Imagine a compra de produtos em promoção, o preparo de uma receita para um número maior de pessoas ou o cálculo do consumo de combustível em uma viagem. Em cada um desses cenários, a regra de três simples se apresenta como uma ferramenta eficaz para a resolução de problemas.Um pacote de biscoitos custa R$ 5,00 e contém 20 unidades.
Se você precisar de 50 biscoitos para uma festa, quanto deverá gastar? Neste caso, estabelecemos uma proporção entre o número de biscoitos e o preço. Aplicando a regra de três simples, descobrimos que 50 biscoitos custarão R$ 12,
50. Outro exemplo
uma receita de bolo que serve 6 pessoas utiliza 200g de farinha. Se você precisar fazer um bolo para 12 pessoas, precisará dobrar a quantidade de farinha, utilizando 400g. Por fim, um carro percorre 15 km com 1 litro de gasolina. Para uma viagem de 120 km, você precisará calcular quantos litros serão necessários, chegando ao resultado de 8 litros.
Construção de um Problema de Regra de Três Simples
Para construir um problema eficaz de regra de três simples, precisamos seguir um roteiro claro e objetivo. Primeiro, definimos um contexto real e relevante, como uma situação de compra, consumo ou receita. Em seguida, apresentamos os dados conhecidos, duas grandezas que estão relacionadas proporcionalmente. Por fim, formulamos uma pergunta que requer o cálculo de um valor desconhecido, baseado na proporcionalidade entre as grandezas.Por exemplo: “Maria está fazendo brigadeiros para uma festa.
Sua receita rende 20 brigadeiros com 1 lata de leite condensado. Se ela precisar de 60 brigadeiros, quantas latas de leite condensado precisará usar?”. Neste problema, o contexto é o preparo de brigadeiros, os dados conhecidos são a quantidade de brigadeiros e a quantidade de leite condensado na receita original, e a pergunta solicita a quantidade de leite condensado necessária para 60 brigadeiros.
Problemas com Diferentes Níveis de Dificuldade
A regra de três simples pode ser aplicada em problemas com diferentes graus de complexidade. Problemas básicos envolvem uma relação direta e simples entre duas grandezas. Problemas intermediários podem incluir conversões de unidades ou múltiplas etapas de cálculo. Problemas avançados podem envolver relações inversamente proporcionais ou múltiplas grandezas.Exemplo básico: “Se 3 maçãs custam R$ 2,00, quanto custam 6 maçãs?”.
Exemplo intermediário: “Um carro percorre 20 km/litro. Quantos litros de combustível são necessários para uma viagem de 300 km, considerando uma perda de 10% no consumo devido a condições adversas?”. Exemplo avançado: “Três pintores pintam uma casa em 5 dias. Se adicionarmos mais dois pintores, quantos dias serão necessários para pintar a mesma casa, considerando que o ritmo de trabalho se mantém constante?”.
Representação Gráfica da Relação entre Grandezas

A visualização gráfica da relação entre as grandezas em um problema de regra de três simples facilita a compreensão e a resolução. Podemos representar essa relação usando blocos de texto, simulando um gráfico de barras.Imagine um problema onde 2 operários constroem uma parede em 6 dias. Podemos representar isso graficamente:| Operários | Dias ||—|—|| 2 | 6 || 4 | X |Neste gráfico, cada bloco representa uma unidade de grandeza.
A altura dos blocos representa a quantidade de operários, e a largura representa o número de dias. A relação entre as grandezas é diretamente proporcional: se o número de operários dobra, o número de dias diminui pela metade.

